眾多的試驗工作中發現，金屬硬度越高，材料強度越大，為了找出洛氏硬度和拉伸強度這兩個變量在一定范圍內存在的關系，選取16組石油鉆桿管體試樣，通過機加工分別制備成拉伸試樣與洛氏硬度試樣，并進行拉伸試驗和洛氏硬度試驗。
一、試樣制備與試驗方法
1、洛氏硬度試樣的制備
圖1：洛氏硬度試樣宏觀形貌
按GB/T 230.1-2018«金屬材料洛氏硬度試驗第1部分：試驗方法»規定進行制備，洛氏硬度試樣如圖1所示。
2、洛氏硬度試驗方法
依據GB/T 230.1-2018，試驗在室溫下(10~35℃)進行，因為溫度的變化可能會對試驗結果有影響。試驗臺應平穩地放在剛性支承物上，表面不得有鐵屑及其他臟物，并使壓頭軸線與試樣表面垂直，避免產生位移。使壓頭與試樣表面接觸，無沖擊和振動下均勻地施加初始試驗力F0，初始試驗力保持時間不應超過3s，從初始試驗力F0施加至總試驗力F的時間應不小于1s且不大于8s?？傇囼灹保持時間為(4±2)s。然后卸除主試驗力F1，保持初始試驗力F0，經過短時間穩定后，讀數并記錄，每組測試16點洛氏硬度，取平均值，試驗結果見表1。
3、拉伸試樣的制備
圖2：拉伸試樣宏觀形貌
按GB/T 228.1-2010«金屬材料拉伸試驗第1部分：室溫試驗方法»中附錄E規定制成全壁厚縱向矩形試樣，如圖2所示。
4、拉伸試驗方法
所用拉伸試驗機型號為TSKL-600W，引伸計型號為FS-004，級別為0.5級，標距為50mm，試驗控制軟件為IDEAR TEST 2010 WincoTechnology Inc.，試驗溫度為(23±5)℃。試驗時確保被夾持試樣受軸向拉力的作用，避免斜拉，斜拉有可能使被測試樣受力不均勻，從而影響試驗結果的準確性。試驗速度控制模式為位移控制，橫梁位移速度為1.5mm·min-1，拉伸試驗結果見表1。
表1：拉伸和洛氏硬度試驗結果
二、試驗結果分析
1、散布圖
為了研究洛氏硬度與抗拉強度之間的關系，根據試驗數據畫出散布圖，橫坐標為洛氏硬度，縱坐標為對應的抗拉強度，如圖3所示。
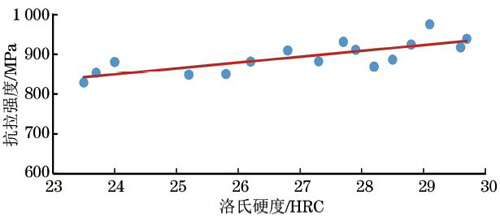圖3：洛氏硬度與抗拉強度的散布圖
由圖3可知，當材料的洛氏硬度增加時，其抗拉強度也呈上升趨勢。因此，可用回歸分析法來分析洛氏硬度與拉伸強度之間的關系。
2、相關系數
由圖3可知，16個測試點基本在一條直線附近，但又不完全在一條直線上，為了表示洛氏硬度與抗拉強度之間線性關系的密切程度，用統計量r來表示兩個變量的相關系數
相關系數公式
式中：x表示洛氏硬度，y表示抗拉強度。
r>0，表示兩個變量正相關，即x越大y就有增大的趨勢；r<0，表示兩個變量負相關，即x越大y就有減小的趨勢；r=0，表示兩個變量不相關，但是有可能存在某種特殊的曲線關系。由于相關系數是根據樣本求出來的，即使兩個變量不相關，但是求出來的相關系數也不一定恰好等于0。
3、相關系數的檢驗
經過計算可得r=0.78。查閱表2檢驗相關系數的臨界值，由于計算得出的r>0.497，即試驗計算得到的數據落在拒絕域區域， 洛氏硬度與抗拉強度存在正線性相關關系。
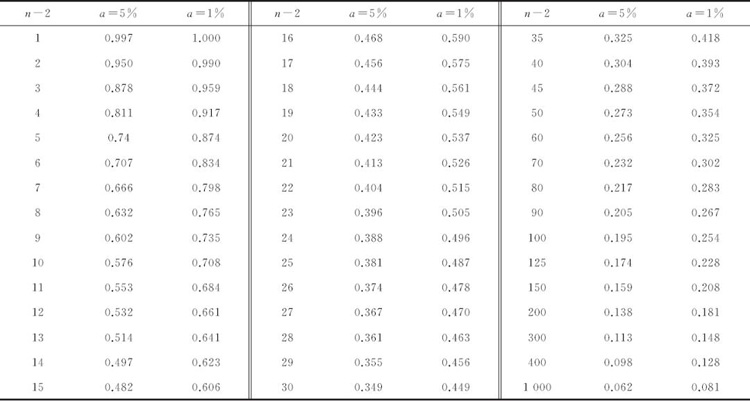
表2：檢驗相關系數的臨界值表
經過計算后課求得的一元線性回歸方程為：
y =496.55+14.704x (2)
4、一元線性回歸方程的顯著性檢驗
建立回歸方程的目的，是為了將兩個具有線性關系的變量用公式表達出來，由于數據來源于試驗，試驗中不可避免地會產生誤差?？梢酝ㄟ^統計技術方法如方差分析對所求得的方程進行顯著性檢驗，即檢驗所求得的方程是否有意義。
試驗中造成數據波動的原因有兩個：一個是由于自變量x的取值不同，得到不同的y值；另一個是除了自變量x以外的一切因素，統稱為隨機誤差。
經計算， a=0.05水平上回歸方程是顯著的。
5、利用回歸方程進行預測
當洛氏硬度值為28.1時，能有置信度為95%概率的把握，預測抗拉強度為852.92~966.54MPa，預測區間示意圖如圖4所示。
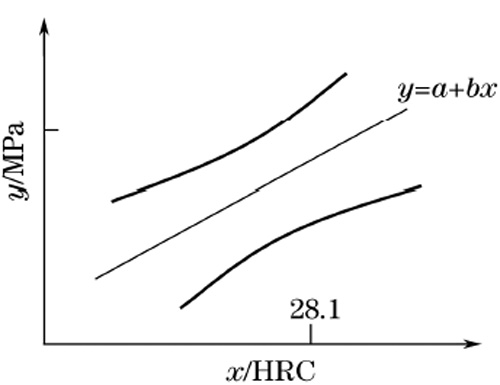
圖4：預測區間圖
由圖4可知，當x0越靠近時，區間寬度越窄，預測的精度越高。
文中樣本空間n僅取16，所取硬度范圍為21~30HRC，實際中的抗拉強度與洛氏硬度之間的回歸問題應取足夠的樣本空間，從而建立起回歸關系式。
6、結論
(1)任何強度?硬度換算表都不可能詳細給出任意硬度?抗拉強度的換算值，所以對大量試驗數據進行計算機回歸處理，得到拉伸強度與洛氏硬度之間的回歸關系是有實際意義的。
(2)洛氏硬度與抗拉強度之間不應是直線關系而應是曲線關系，但在一定范圍內可以近似看作線性關系。
(3)所得到的回歸關系式為y=496.55+14.704x，在生產條件固定的情況下，洛氏硬度檢測快速?簡便，對于某些不能進行拉伸試驗也不便進行布氏硬度試樣和儀器壓痕試驗的材料，可以通過預先得到的回歸方程估算其抗拉強度。
來源：天氏庫力 發布日期
2022-04-26 瀏覽：
